이전 포스팅에서 그래프 탐색 이론 중 하나인 DFS (깊이 우선 탐색) 에 대해 배우고, 실제 구현하는 코드를 살펴보았다.
그래프 탐색 알고리즘 - DFS (깊이 우선 탐색) 코드 구현
[자료구조C#] 그래프 탐색 알고리즘 - DFS (깊이 우선 탐색) 코드 구현
위 포스팅에서 우리는 그래프 예시를 통해 DFS가 무엇인지에 대해 이해했다.이제 실제로 이 인물 관계도 그래프와 DFS를 C# 코드로 구현해보자.지난 포스팅에서도 잠깐 살펴 보았지만, 우선 이 인
nybot-house.tistory.com
이번 포스팅에서는 그래프 탐색 이론 중 하나인 BFS (Breadth-First Search, 너비 우선 탐색)에 대해 알아보자.
BFS 너비 우선 탐색이란?
BFS는 그래프 탐색 알고리즘 중 하나로, 시작 정점에서 출발하여 가까운 정점들부터 탐색하는 방법이다.
이전과 같은 가상의 인물 관계도를 다시 보며 생각해 보자.
필자는 관계도의 모든 인물들과 데이트를 하고 싶다. BFS 탐색 방법을 사용한다면 순서가 어떻게 될까?
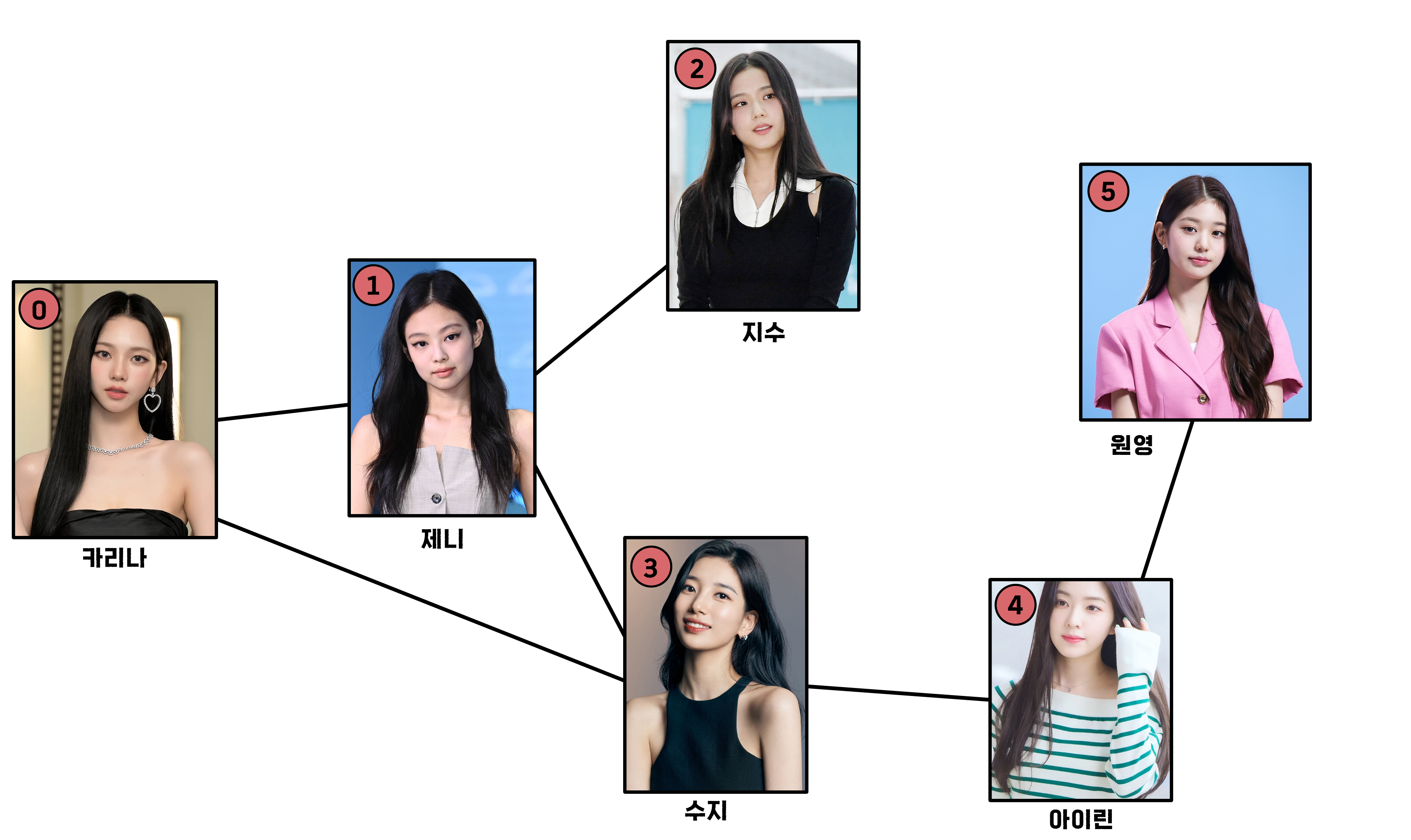
오늘은 먼저 0번 카리나부터 방문을 시작해 보자. 그리고 오늘은 다시는 없을 기회, 신중하게 접근하려고 한다. 따라서 BFS를 사용해 순회해볼 것이다.
BFS 기본 개념
- 큐(Queue): BFS는 주로 큐를 사용하여 구현된다. 큐는 선입선출(FIFO, First In First Out) 방식으로 동작한다.
(*큐의 특징을 이해해야 BFS를 이해할 수 있다.) - 방문(visited): 각 정점이 방문되었는지를 기록한다.
- 탐색 순서: 시작 정점에서 인접한 정점들을 모두 큐에 넣고, 큐에서 하나씩 꺼내면서 다시 그 정점과 인접한 정점들을 큐에 넣는 방식으로 진행된다.
BFS의 특징
- 레벨 단위 탐색: BFS는 가장 가까운 정점부터 차례대로 탐색하므로, 탐색 과정에서 정점은 탐색 깊이에 따라 레벨이 나뉜다.
- 최단 경로: 가중치가 없는 그래프에서 BFS는 시작 정점에서 다른 모든 정점으로 가는 최단 경로를 찾는데 유용하다.
- 시간 복잡도: O(V+E) - V는 정점의 수, E는 간선의 수.
BFS 구현
위의 소셜 네트워킹 관계도를, 이전과 같이 그래프로 구현해 보고, BFS 코드를 구현해 보았다.
using System.Reflection.Metadata;
namespace Exercise
{
//스택: LIFO(후입선출 Last In First Out)
//큐: FIFO(선입선출 First In First Out)
class Graph
{
//모든 정보를 들고 있는 방식, 배열 사용
int[,] adj = new int[6, 6]
{
{0, 1, 0, 1, 0, 0}, //0번 카리나 정점 연결 정보
{1, 0, 1, 1, 0, 0}, //1번 제니 정점 연결 정보
{0, 1, 0, 0, 0, 0}, //2번 지수 정점 연결 정보
{1, 1, 0, 0, 1, 0}, //3번 수지 정점 연결 정보
{0, 0, 0, 1, 0, 1}, //4번 아이린 정점 연결 정보
{0, 0, 0, 0, 1, 0}, //5번 원영 정점 연결 정보
//팁 - 배열을 유심히 보면 대각선 방향으로 대칭됨 (양방향으로 연결되어 있는 그래프이기 때문)
};
public void BFS(int start)
{
bool[] found = new bool[6];
Queue<int> que = new Queue<int>();
que.Enqueue(start);
found[start] = true;
while (que.Count > 0)
{
int now = que.Dequeue();
Console.WriteLine(now);
for (int next = 0; next < 6; next++)
{
if (adj[now, next] == 0)
continue;
if (found[next])
continue;
que.Enqueue(next);
found[next] = true;
}
}
}
}
class Program
{
static void Main(string[] args)
{
//BFS (Breadth First Search 너비 우선 탐색)
Graph graph = new Graph();
graph.BFS(0);
}
}
}
카리나(0) -> 제니(1) -> 수지(3) -> 지수(2) -> 아이린(4) -> 원영(5) 순서로 방문하게 된다.
DFS는 다양한 용도로 사용되는 반면, BFS는 일반적으로 길 찾기 용도로만 사용된다.
또한 BFS에는 그 부모 정점은 누구인지, 정점 간의 거리는 얼마인지 등의 다양한 정보도 삽입하여 추출할 수 있다.
이번에는 소셜 네트워크 관계도에서 각자 가장 친한 사람이 있다고 가정해 보고, 또한 각자의 거주지의 거리 정보가 저장되어 있다고 가정해 보자.
using System.Reflection.Metadata;
namespace Exercise
{
//스택: LIFO(후입선출 Last In First Out)
//큐: FIFO(선입선출 First In First Out)
class Graph
{
//모든 정보를 들고 있는 방식, 배열 사용
int[,] adj = new int[6, 6]
{
{0, 1, 0, 1, 0, 0}, //0번 카리나 정점 연결 정보
{1, 0, 1, 1, 0, 0}, //1번 제니 정점 연결 정보
{0, 1, 0, 0, 0, 0}, //2번 지수 정점 연결 정보
{1, 1, 0, 0, 1, 0}, //3번 수지 정점 연결 정보
{0, 0, 0, 1, 0, 1}, //4번 아이린 정점 연결 정보
{0, 0, 0, 0, 1, 0}, //5번 원영 정점 연결 정보
//팁 - 배열을 유심히 보면 대각선 방향으로 대칭됨 (양방향으로 연결되어 있는 그래프이기 때문)
};
public void BFS(int start)
{
bool[] found = new bool[6];
int[] bestie = new int[6];
int[] distance = new int[6];
Queue<int> que = new Queue<int>();
que.Enqueue(start);
found[start] = true;
bestie[start] = start;
distance[start] = 0;
while (que.Count > 0)
{
int now = que.Dequeue();
Console.WriteLine(now);
for (int next = 0; next < 6; next++)
{
if (adj[now, next] == 0) //인접하지 않았다면 (경로가 없다면) 스킵
continue;
if (found[next]) //이미 방문한 사람이라면 스킵
continue;
que.Enqueue(next);
found[next] = true;
bestie[next] = now;
distance[next] = distance[now] + 1;
}
}
}
}
class Program
{
static void Main(string[] args)
{
//BFS (Breadth First Search 너비 우선 탐색)
Graph graph = new Graph();
graph.BFS(0);
}
}
}위 코드처럼 bestie 와 distance 라는 정보를 BFS() 메서드 내에 관련 로직을 추가하여 저장하고 추출해 낼 수 있다.
'C# 자료구조, 알고리즘, 길찾기 > 그래프' 카테고리의 다른 글
| [자료구조C#] 그래프 탐색 알고리즘 - DFS (깊이 우선 탐색) 코드 구현 (0) | 2024.06.11 |
|---|---|
| [자료구조C#] 그래프 탐색 알고리즘- DFS (깊이 우선 탐색) 개론 (0) | 2024.06.11 |
| [자료구조] 그래프 개요 (0) | 2024.06.11 |
