위 포스팅에서 우리는 그래프 예시를 통해 DFS가 무엇인지에 대해 이해했다.
이제 실제로 이 인물 관계도 그래프와 DFS를 C# 코드로 구현해보자.
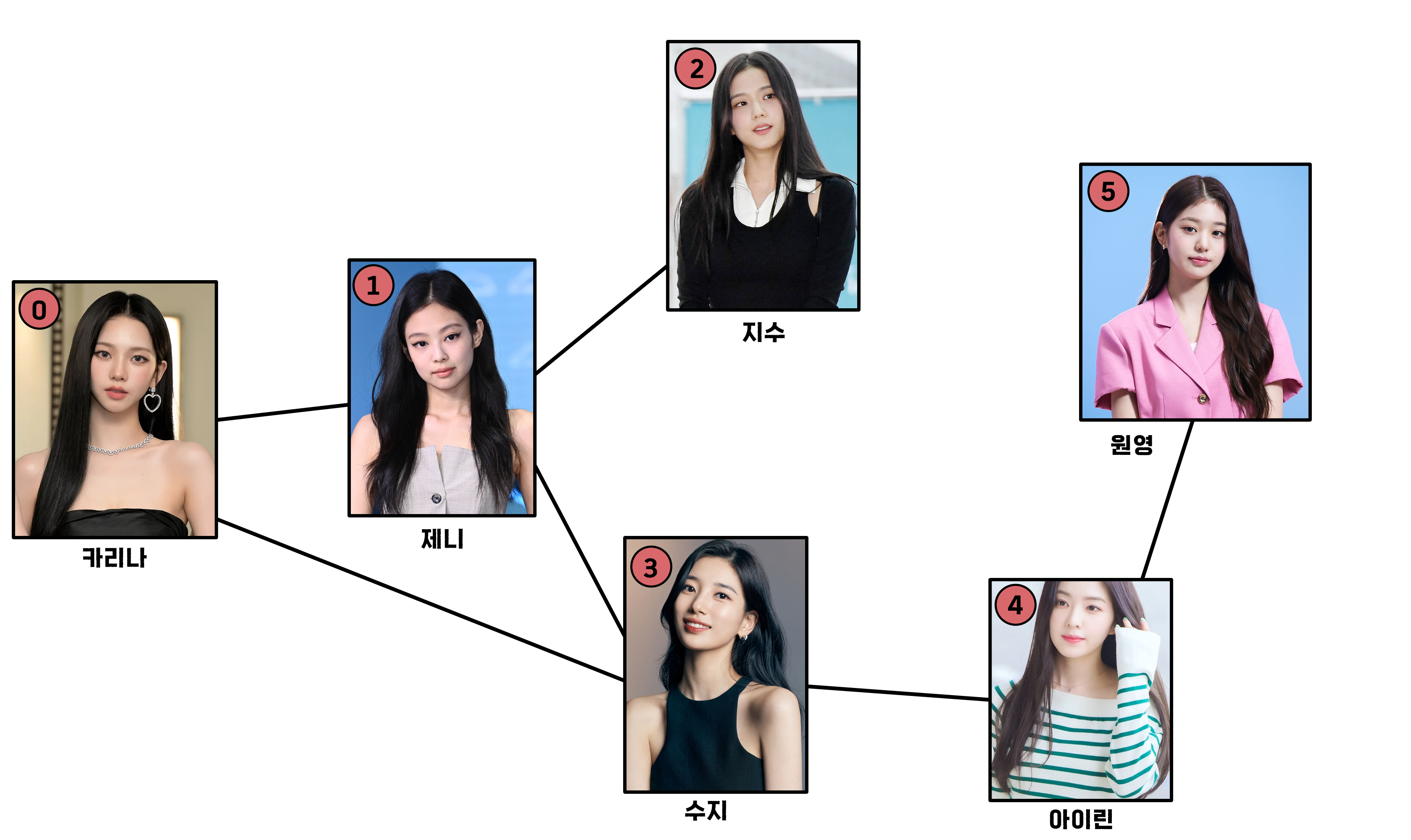
지난 포스팅에서도 잠깐 살펴 보았지만, 우선 이 인물 관계도를 그래프로 구현하는 방법에는 크게 2가지가 있다. 배열을 사용해 인접 행렬을 만드는 방법과, 리스트 배열을 사용해서 인접 리스트를 만드는 방법이다.
class Graph
{
//모든 정보를 들고 있는 방식, 배열 사용
int[,] adj = new int[6, 6]
{
{0, 1, 0, 1, 0, 0}, //0번 카리나 정점 연결 정보
{1, 0, 1, 1, 0, 0}, //1번 제니 정점 연결 정보
{0, 1, 0, 0, 0, 0}, //2번 지수 정점 연결 정보
{1, 1, 0, 0, 1, 0}, //3번 수지 정점 연결 정보
{0, 0, 0, 1, 0, 1}, //4번 아이린 정점 연결 정보
{0, 0, 0, 0, 1, 0}, //5번 원영 정점 연결 정보
//팁 - 배열을 유심히 보면 대각선 방향으로 대칭됨 (양방향으로 연결되어 있는 그래프이기 때문)
};
//필요한 인덱스 정보만 들고 있는 방식, 리스트 배열 사용
List<int>[] adj2 = new List<int>[]
{
new List<int>() { 1, 3 }, //0번 카리나 정점 연결 정보
new List<int>() { 0, 2, 3}, //1번 제니 정점 연결 정보
new List<int>() { 1 }, //2번 지수 정점 연결 정보
new List<int>() { 0, 1, 4 }, //3번 수지 정점 연결 정보
new List<int>() { 3, 5 }, //4번 아이린 정점 연결 정보
new List<int>() { 4 }, //5번 원영 정점 연결 정보
};
}adj 배열에서는 각각의 정점 연결 정보를 0이면 연결되어 있지 않음, 1이면 연결되어 있음으로 표시했다.
adj2 리스트 배열에서는 각각의 연결 정보를 숫자로 표시해 주었다. 배열의 각 인덱스는 특정 정점(인물)을 나타내고, 그 인덱스에 해당하는 리스트는 해당 정점(인물)과 연결된 정점들(인물들)을 나타낸다. 예를 들어 adj2[0]은 정점 0(카리나)와 연결된 정점들을 나타내며, 1(제니)와 3(수지)와 연결되어 있다.
우선 adj를 순회할 DFS 메서드를 만들어 보자.
bool[] visited = new bool[6];
// 1) 우선 here부터 방문
// 2) here와 연결된 정점들을 하나씩 확인해서, [아직 미방문 상태라면] 방문.
public void DFS(int here)
{
Console.WriteLine(here); // 현재 정점 출력
visited[here] = true; // 현재 정점을 방문했음을 표시
for (int next = 0; next < adj.GetLength(0); next++)
{
if (adj[here, next] == 0) // 연결되어 있지 않으면 스킵
continue;
if (visited[next]) // 이미 방문한 정점이면 스킵
continue;
DFS(next); // 연결된 정점을 재귀적으로 방문
}
}DFS 함수는 현재 정점(here)을 방문하고, 연결된 정점을 재귀적으로 방문한다. 로직은 다음과 같다.
(*재귀 함수: 자기 자신을 호출하는 프로그래밍 기법)
- 시작 정점을 방문하고 출력한다. 'Console.WriteLine(here)'
- 방문한 정점을 기록한다. 'visited[here] = true'
- 현재 정점에 연결된 모든 정점을 확인한다. 'for()...'
- 방문하지 않은 정점이 있으면 해당 정점으로 이동하여 DFS를 재귀적으로 수행한다. 'DFS(next)'
(이미 방문한 정점은 스킵) - 더 이상 방문할 정점이 없으면 재귀를 종료하고 이전 정점으로 돌아간다.
이전 포스팅에서 살펴보았듯이 제니(1)부터 방문했을 경우 DFS 로직에 따르면 방문 순서가
제니(1) -> 카리나(0) -> 수지(3) -> 아이린(4) -> 원영(5) -> 지수(2)
이렇게 되었었는데, 실제 프로그램 실행 결과도 동일한지 살펴보자.
using System.Reflection.Metadata;
namespace Exercise
{
class Graph
{
//모든 정보를 들고 있는 방식, 배열 사용
int[,] adj = new int[6, 6]
{
{0, 1, 0, 1, 0, 0}, //0번 카리나 정점 연결 정보
{1, 0, 1, 1, 0, 0}, //1번 제니 정점 연결 정보
{0, 1, 0, 0, 0, 0}, //2번 지수 정점 연결 정보
{1, 1, 0, 0, 1, 0}, //3번 수지 정점 연결 정보
{0, 0, 0, 1, 0, 1}, //4번 아이린 정점 연결 정보
{0, 0, 0, 0, 1, 0}, //5번 원영 정점 연결 정보
//팁 - 배열을 유심히 보면 대각선 방향으로 대칭됨 (양방향으로 연결되어 있는 그래프이기 때문)
};
bool[] visited = new bool[6];
// 1) 우선 here부터 방문
// 2) here와 연결된 정점들을 하나씩 확인해서, [아직 미방문 상태라면] 방문.
public void DFS(int here)
{
Console.WriteLine(here); // 현재 정점 출력
visited[here] = true; // 현재 정점을 방문했음을 표시
for (int next = 0; next < adj.GetLength(0); next++)
{
if (adj[here, next] == 0) // 연결되어 있지 않으면 스킵
continue;
if (visited[next]) // 이미 방문한 정점이면 스킵
continue;
DFS(next); // 연결된 정점을 재귀적으로 방문
}
}
}
class Program
{
static void Main(string[] args)
{
//DFS (Depth First Search 깊이 우선 탐색)
//BFS (Breadth First Search 너비 우선 탐색)
Graph graph = new Graph();
graph.DFS(1);
}
}
}
제니(1) -> 카리나(0) -> 수지(3) -> 아이린(4) -> 원영(5) -> 지수(2) 로 결과는 같은 것을 확인할 수 있다.
이번에는 adj2 를 사용해서 adj와 똑같은 결과가 나오는지 확인해 보자.
using System.Reflection.Metadata;
namespace Exercise
{
//스택: LIFO(후입선출 Last In First Out)
//큐: FIFO(선입선출 First In First Out)
class Graph
{
//모든 정보를 들고 있는 방식, 배열 사용
int[,] adj = new int[6, 6]
{
{0, 1, 0, 1, 0, 0}, //0번 카리나 정점 연결 정보
{1, 0, 1, 1, 0, 0}, //1번 제니 정점 연결 정보
{0, 1, 0, 0, 0, 0}, //2번 지수 정점 연결 정보
{1, 1, 0, 0, 1, 0}, //3번 수지 정점 연결 정보
{0, 0, 0, 1, 0, 1}, //4번 아이린 정점 연결 정보
{0, 0, 0, 0, 1, 0}, //5번 원영 정점 연결 정보
//팁 - 배열을 유심히 보면 대각선 방향으로 대칭됨 (양방향으로 연결되어 있는 그래프이기 때문)
};
//필요한 인덱스 정보만 들고 있는 방식, 리스트 배열 사용
List<int>[] adj2 = new List<int>[]
{
new List<int>() { 1, 3 }, //0번 카리나 정점 연결 정보
new List<int>() { 0, 2, 3}, //1번 제니 정점 연결 정보
new List<int>() { 1 }, //2번 지수 정점 연결 정보
new List<int>() { 0, 1, 4 }, //3번 수지 정점 연결 정보
new List<int>() { 3, 5 }, //4번 아이린 정점 연결 정보
new List<int>() { 4 }, //5번 원영 정점 연결 정보
};
bool[] visited = new bool[6];
// 1) 우선 here부터 방문
// 2) here와 연결된 정점들을 하나씩 확인해서, [아직 미방문 상태라면] 방문.
public void DFS(int here)
{
Console.WriteLine(here); // 현재 정점 출력
visited[here] = true; // 현재 정점을 방문했음을 표시
for (int next = 0; next < adj.GetLength(0); next++)
{
if (adj[here, next] == 0) // 연결되어 있지 않으면 스킵
continue;
if (visited[next]) // 이미 방문한 정점이면 스킵
continue;
DFS(next); // 연결된 정점을 재귀적으로 방문
}
}
public void DFS2(int here)
{
Console.WriteLine(here);
visited[here] = true;
foreach(int next in adj2[here])
{
if (visited[next])
continue;
DFS2(next);
}
}
}
class Program
{
static void Main(string[] args)
{
//DFS (Depth First Search 깊이 우선 탐색)
//BFS (Breadth First Search 너비 우선 탐색)
Graph graph = new Graph();
graph.DFS2(1);
}
}
}DFS2() 는 인접 리스트를 사용하여 깊이 우선 탐색을 구현해 본 메서드이다. 이 방식은 현재 정점과 직접 연결된 정점만 순회하는 방식이다. (DFS는 모든 정점을 순회하면서 연결 여부를 확인해 보았었다.)
코드를 실행해 보면 DFS()와 DFS2()는 같은 탐색 순서 결과가 나오는 것을 확인할 수 있다.
- 제니(1) -> 카리나(0) -> 수지(3) -> 아이린(4) -> 원영(5) -> 지수(2) (이미 방문한 정점은 스킵)

다만 두 가지 방식에는 다음과 같은 차이점이 있다.
인접 행렬 VS 인접 리스트
인접 행렬
- 구현 방식: 2차원 배열을 사용하여 그래프를 표현합니다.
- 장점:
- 간선의 존재 여부를 O(1) 시간에 확인할 수 있습니다.
- 그래프의 정점 수가 적고 간선 수가 많은 경우(즉, 밀집 그래프(Dense Graph))에 효율적입니다.
- 단점:
- 메모리 사용량이 많습니다. V×VV \times V 크기의 배열이 필요하므로, 간선의 수가 적은 경우(즉, 희소 그래프(Sparse Graph)) 비효율적입니다.
- 모든 정점을 순회해야 하므로 시간 복잡도가 O(V^2)입니다.
인접 리스트
- 구현 방식: 각 정점에 연결된 정점들을 리스트로 표현합니다.
- 장점:
- 메모리 사용량이 적습니다. 정점의 수가 많고 간선의 수가 적은 경우(희소 그래프)에 효율적입니다.
- 정점과 연결된 정점만 순회하므로 시간 복잡도가 O(V + E)입니다.
- 단점:
- 간선의 존재 여부를 확인하는 데 O(V) 시간이 걸릴 수 있습니다.
즉, 인접 리스트를 사용하는 이유는 메모리 효율성과 탐색 효율성 때문이다. 인접 리스트는 정점과 연결된 정점들만 저장하므로, 정점의 수가 많고 간선의 수가 적은 경우 메모리를 효율적으로 사용할 수 있다. 또한 연결된 정점만 순회하므로 탐색 속도가 빨라진다. 특히 DFS와 같은 알고리즘에서는 현재 정점과 연결된 정점만 탐색하면 되므로 효율적이다.
'C# 자료구조, 알고리즘, 길찾기 > 그래프' 카테고리의 다른 글
| [자료구조C#] 그래프 탐색 알고리즘 - BFS 너비 우선 탐색 (0) | 2024.06.12 |
|---|---|
| [자료구조C#] 그래프 탐색 알고리즘- DFS (깊이 우선 탐색) 개론 (0) | 2024.06.11 |
| [자료구조] 그래프 개요 (0) | 2024.06.11 |
